In Dr. Jacek Marczyk, I gained a partner over 15 years ago who has been dealing with the problems of complexity and risk management in high-risk industries for many years.
As part of my research and published in "Interdependency", I developed a new set of tools for the quantitative measurement of dynamic complexity and systems for shaping and managing the viability of companies.
The AI developed by Dr. Jacek Marczyk makes a valuable contribution to examining large amounts of data with regard to their interdependencies. The result of our collaboration lies above all in the transfer of OntoSpace® AI from primarily technical application areas in engineering to open-industry applications for companies and organizations as well as systems of all kinds.
The OntoSpace® AI is extremely helpful for determining and analyzing the parameters relevant to the LIFE CAPABILITY AXIS of my strategy cube.
With their help, not only early warning systems and effective risk management, but also business models and strategies can be successfully developed and managed in a complex environment.
The complexity metric: structure, entropy and data granularity
The Ontonix metric on which my work is based takes into account all the components required for a solid and comprehensive complexity measure: Structure, entropy, and data granularity or coarseness.
- Entropy is a measure of the disorder or uncertainty in a system. In information theory, entropy is often used to describe the average amount of information in a data set. The higher the entropy, the greater the unpredictability or disorder of the data.
- Data granularity refers to the size or resolution of the data that is available or being analyzed. It refers to the fineness or accuracy of the data being viewed in a particular context. The finer the granularity, the more details or differences are captured in the data.
Complexity as a measurable quantity
I view complexity as a quantity of structured information and therefore as a measurable quantity, comparable to mass, energy or frequency.
- Complexity has many positive sides, especially when it comes to making systems and organizations more adaptable, resilient and innovative. Here are some of the most important positive aspects of complexity:
- Adaptability: Complex systems can adapt better to changes in their environment. This is because they have diverse components and interactions that enable different solutions and reactions to new challenges.
- Resilience: Complex systems are often more resilient to disruptions and failures because they have multiple ways and mechanisms to respond to problems. For example, a complex network of communication systems can withstand the failure of individual components better than a simple, monolithic system.
- Innovation: Complex systems offer a multitude of paths and opportunities for innovation. The interaction between different components and players can lead to new ideas, technologies and processes. In a company, different departments and teams can work together to develop innovative solutions.
- Creativity: Complex systems promote creativity because they integrate different perspectives and skills. Breakthrough ideas often emerge in a creative environment characterized by diversity and interdisciplinarity.
- Efficiency: Complex systems can work more efficiently thanks to specialized components and optimized processes. Each part of the system can be optimized for its specific task, resulting in better overall performance. For example, in a complex supply chain, each step from production to delivery can be precisely coordinated and optimized.
- Optimization: By using data analysis and machine learning, complex systems can be constantly monitored and improved. This enables continuous optimization and adaptation to new conditions.
- Robustness: Complex systems are often more robust against errors and failures. Due to the redundancy and diversity in their components, they can better compensate for failures of individual parts. For example, a complex IT network can reroute data traffic if a server fails.
- Fault tolerance: In a complex system, fault tolerance can be increased by implementing multiple paths and backup systems. This means that an error in one part of the system does not necessarily paralyze the entire system.
- Scalability: Complex systems are often more scalable as they consist of modular components that can be expanded or replaced independently of each other. For example, a company can grow by introducing new departments or technologies without having to change the entire structure.
- Growth: Complexity enables systems to grow and develop. By integrating new elements and creating new connections, the system can handle larger and more diverse tasks.
Critical complexity: An important limit
An important aspect is the conceptualization of critical complexity limits. A system cannot be more complex than its critical complexity unless additional structures are added. Close to these critical complexity limits, systems become particularly fragile and can suddenly collapse.
Quantitative approaches in complexity research
A well-founded metric makes it possible to go beyond mere speculation and create a basis for meaningful scientific investigations and practical complexity management.
The role of the metric as a bridge between physics and information theory
The metric acts as a bridge between physics and information theory by capturing not only the dynamic interaction between structure and entropy, but also the amount of information that results from the structure.
Interaction between structure and entropy
Although structure and entropy represent opposing tendencies, they are intertwined and influence each other in complex ways:
- Dynamic equilibrium: In many systems, there is a dynamic equilibrium between the creation of structure and the increase in entropy. Living organisms, for example, maintain their structure (order) through a continuous supply of energy, which, however, also generates entropy.
- Energy and information: Structure requires energy and information to be maintained. Maintaining or creating structure reduces entropy locally, but can increase entropy globally. For example, a refrigerator uses energy to maintain a low temperature (low entropy) within the appliance, while the environment experiences higher entropy due to the heat dissipated.
- Evolution and innovation: In evolutionary processes, the creation of new structures leads to an increase in complexity. These new structures must deal efficiently with entropy in order to remain stable. Innovations often arise through the increase in structural complexity, which is, however, limited by the resulting entropy.
- Critical complexity: A system can only become structurally more complex up to a certain point before entropy destabilizes it. This is referred to as critical complexity. Beyond this point, the system becomes fragile and prone to collapse.
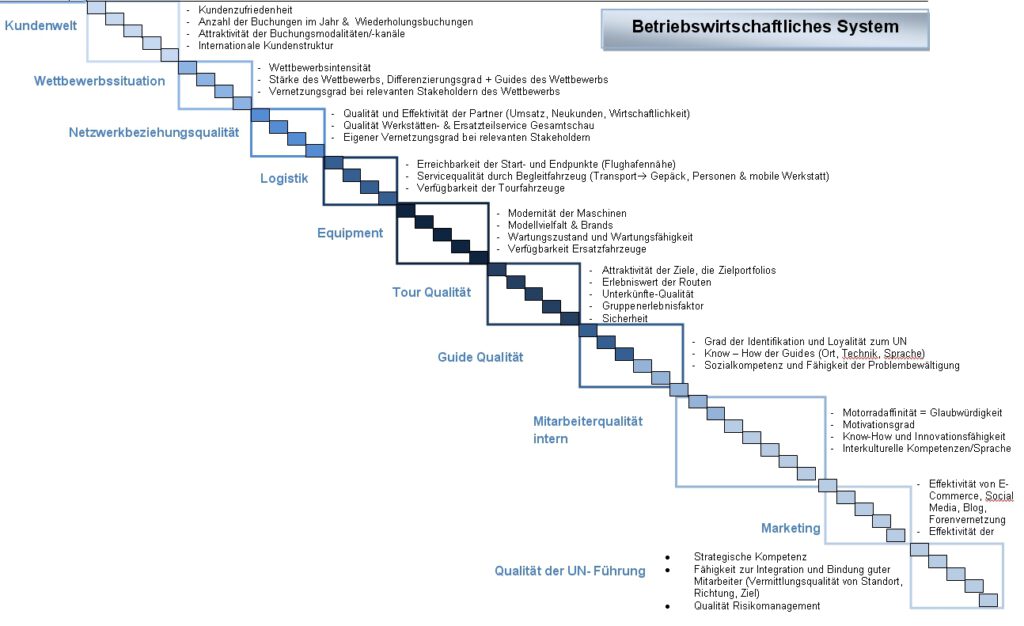
From system DNA to measurable and controllable hub parameters
Step 1: Determining the relevant parameters of a system - examples
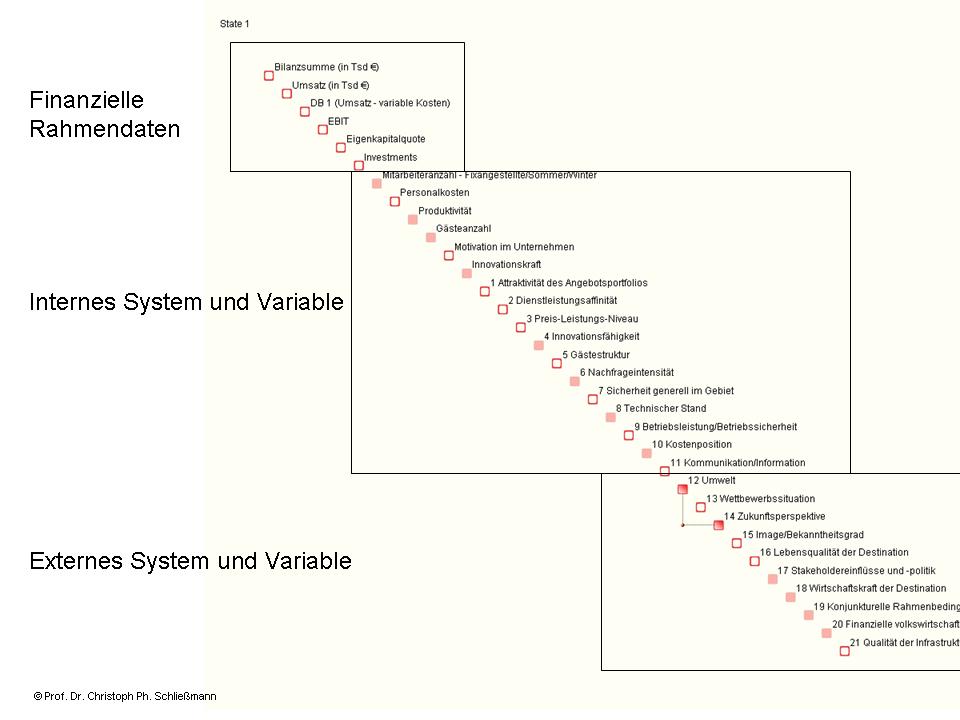
Step 2: Determine quantifiable measurement data for the relevant parameters
Step 3: Complexity metricof the structured information
Step 4: Identify the control hubs in the system - focus on them
With "OntoSpace", the tool for system and complexity analysis that Christoph Schließmann integrated together with his technology partner Ontonix during the development of the interdependency method, it is possible to apply fuzzy logic alongside exact data. Past experience and planning periods for the near future are converted into key figures. The instrument works model-free and the system data determined is processed as it is without model filtering. The key to model-free "analysis" is to "see" the information and not to "analyze" it.
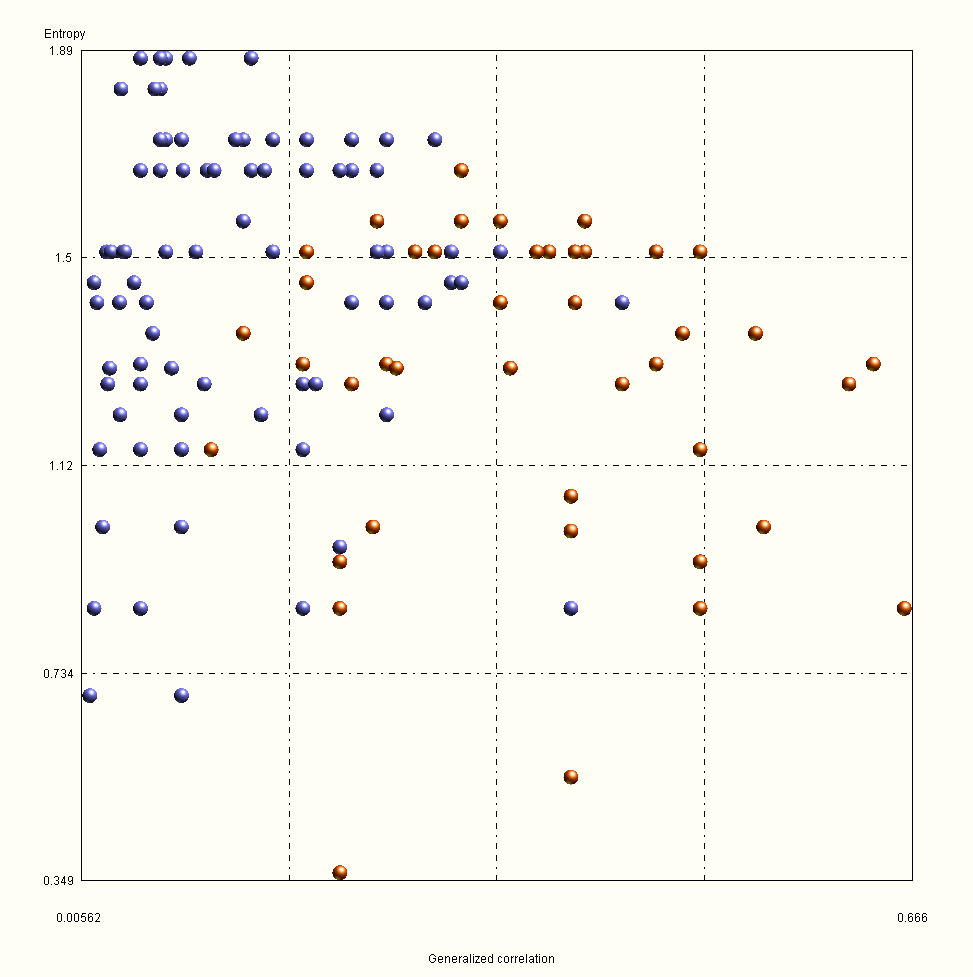
Entropy measures the degree of disorganization of information. OntoSpace processes multidimensional information via its data entropy into a superordinate "image structure", reducing it to pixels. This results in regions with high data density (clusters), zones with very low density, empty regions and some isolated points (outliers). Images with structure transmit more information than chaotic images. Although some images have low entropy - they are very "organized" - they still transmit little information. This is because entropy measures not only the degree of chaos, but also information. A single black pixel has the lowest possible entropy, but at the cost of any missing information. The properties of the system can be determined via the information structures: the presence of complexity as a product of agility and robustness. Statements can be made about which variables contribute to complexity and to what extent, the overall complexity of the system, its minimum and critical limit complexity and its robustness to absorb negative influences. Complexity is identified using a knock-out technique, a quantification process that provides information about the effects of individual variables on the overall complexity of a system. First, the overall complexity of the system is calculated, then each variable is removed from the system and the complexity is recalculated again and again depending on the situation. The difference between the two complexity values is correlated with the original complexity value. The variable is then returned to the system data set and the next variable is removed.
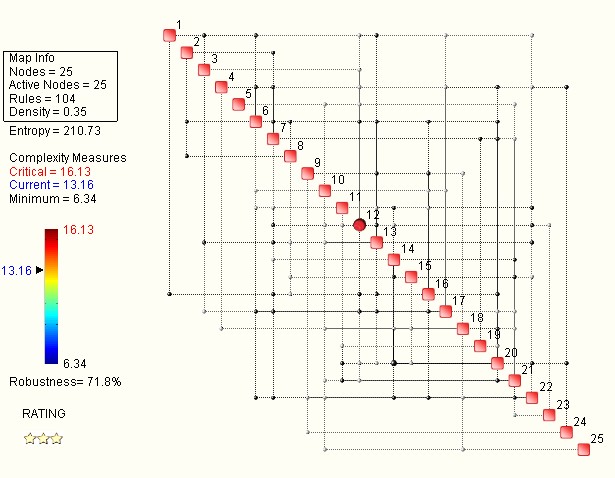
The system rating measures the degree of complexity within a minimum and critical maximum (high fragility of the system), the robustness as well as the degree of agility and shows the HUBS of the greatest interdependence, such as the parameter 12 of 25 in the example of an automotive company.
In this example, the system entropy, i.e. the degree of disorder and uncertainty in the system relations, is relatively high at 210. The more different correlation and arrangement possibilities the parameters in a system offer, the more the degree of entropy increases.
With a minimum of 6, the complexity level is 13 out of 16 points and is therefore in the beginning critical range, which also puts the robustness and resilience level of just under 72% into perspective. Such a system is highly vulnerable!
It is therefore important to scrutinize the critical networks and parameters and to interpret scenarios for the viability of the system in the future.
This rating matrix provides an overview of the interdependencies of the parameters and their contribution to complexity. There is extensive information on each individual relationship.
Each individual interdependency can now be analyzed in terms of relationship quality and entropy: