In Dr. Jacek Marczyk habe ich vor über 15 Jahren einen Partner gewonnen, der sich seit vielen Jahren mit der Problematik der Komplexität und des Risikomanagements in Hochrisikoindustrien beschäftigt.
Im Rahmen meiner Forschungen und in „Interdependency“ publiziert, entstand neu entwickeltes Instrumentarium zur quantitativen Messung von dynamischer Komplexität und Systemen zur Gestaltung und Steuerung der Lebensfähigkeit von Unternehmen.
Die dabei verwendete und von Dr. Jacek Marczyk entwickelte AI/KI leistet einen wertvollen Beitrag große Datenmengen hinsichtlich ihrer Interdependenzen zu untersuchen. Das Ergebnis unserer Zusammenarbeit liegt vor allem im Transfer der OntoSpace® AI von schwerpunktmäßig technischen Anwendungsbereichen im Engineering in die branchenoffene Anwendung für Unternehmen und Organisationen sowie Systemen aller Art.
Für die Bestimmung und Analyse der für die LEBENSFÄHIGKEITS-ACHSE meines Strategie-Würfels relevanten Parameter ist die OntoSpace® AI höchst hilfreich.
Mit ihrer Hilfe können nicht nur Frühwarnungssysteme und ein effektives Risikomanagement, sondern Geschäftsmodelle und Strategien in komplexem Umfeld erfolgreich aufgebaut und gesteuert werden.
Die Komplexitätsmetrik: Struktur, Entropie und Datengranularität
Die meiner Arbeit zugrundeliegende Metrik von Ontonix berücksichtigt alle Bestandteile, die für ein solides und umfassendes Komplexitätsmaß erforderlich sind: Struktur, Entropie und Datengranularität bzw. Grobkörnigkeit.
- Entropie ist ein Maß für die Unordnung oder Unsicherheit in einem System. In der Informationstheorie wird Entropie oft verwendet, um die durchschnittliche Menge an Information in einem Datensatz zu beschreiben. Je höher die Entropie ist, desto größer ist die Unvorhersehbarkeit oder Unordnung der Daten.
- Datengranulität bezieht sich auf die Größe oder die Auflösung der Daten, die zur Verfügung stehen oder analysiert werden. Es bezeichnet die Feinheit oder Genauigkeit der Daten, die in einem bestimmten Kontext betrachtet werden. Je feiner die Granularität ist, desto mehr Details oder Unterschiede werden in den Daten erfasst.
Komplexität als messbare Größe
Ich betrachte Komplexität als Menge und bestimmte Qualität an strukturierter Information und damit als eine messbare Größe, vergleichbar mit Masse, Energie oder Frequenz.
Komplexität hat viele positive Seiten, insbesondere wenn es darum geht, Systeme und Organisationen anpassungsfähiger, widerstandsfähiger und innovativer zu machen. Hier sind einige der wichtigsten positiven Aspekte der Komplexität:
- Anpassungsfähigkeit: Komplexe Systeme können sich besser an Veränderungen in ihrer Umgebung anpassen. Dies liegt daran, dass sie vielfältige Komponenten und Interaktionen haben, die verschiedene Lösungen und Reaktionen auf neue Herausforderungen ermöglichen.
- Resilienz: Komplexe Systeme sind oft widerstandsfähiger gegenüber Störungen und Ausfällen, da sie mehrere Wege und Mechanismen haben, um auf Probleme zu reagieren. Zum Beispiel kann ein komplexes Netzwerk von Kommunikationssystemen den Ausfall einzelner Komponenten besser überstehen als ein einfaches, monolithisches System.
- Innovation: Komplexe Systeme bieten eine Vielzahl von Wegen und Möglichkeiten für Innovationen. Die Interaktion zwischen verschiedenen Komponenten und Akteuren kann zu neuen Ideen, Technologien und Prozessen führen. In einem Unternehmen können unterschiedliche Abteilungen und Teams zusammenarbeiten, um innovative Lösungen zu entwickeln.
- Kreativität: Komplexe Systeme fördern Kreativität, da sie unterschiedliche Perspektiven und Fähigkeiten integrieren. In einem kreativen Umfeld, das durch Vielfalt und Interdisziplinarität geprägt ist, entstehen oft bahnbrechende Ideen.
- Effizienz: Komplexe Systeme können durch spezialisierte Komponenten und optimierte Prozesse effizienter arbeiten. Jedes Teil des Systems kann auf seine spezifische Aufgabe optimiert werden, was insgesamt zu einer besseren Leistung führt. Zum Beispiel kann in einer komplexen Lieferkette jeder Schritt von der Produktion bis zur Auslieferung genau abgestimmt und optimiert werden.
- Optimierung: Durch die Nutzung von Datenanalyse und maschinellem Lernen können komplexe Systeme ständig überwacht und verbessert werden. Dies ermöglicht eine kontinuierliche Optimierung und Anpassung an neue Bedingungen.
- Robustheit: Komplexe Systeme sind oft robuster gegenüber Fehlern und Ausfällen. Durch die Redundanz und Vielfalt in ihren Komponenten können sie Ausfälle einzelner Teile besser kompensieren. Beispielsweise kann ein komplexes IT-Netzwerk Datenverkehr umleiten, wenn ein Server ausfällt.
- Fehlertoleranz: In einem komplexen System kann die Fehlertoleranz erhöht werden, indem mehrere Pfade und Backup-Systeme implementiert werden. Dies bedeutet, dass ein Fehler in einem Teil des Systems nicht zwangsläufig das gesamte System lahmlegt.
- Skalierbarkeit: Komplexe Systeme sind oft besser skalierbar, da sie aus modularen Komponenten bestehen, die unabhängig voneinander erweitert oder ausgetauscht werden können. Ein Unternehmen kann beispielsweise durch die Einführung neuer Abteilungen oder Technologien wachsen, ohne dass die gesamte Struktur verändert werden muss.
- Wachstum: Komplexität ermöglicht es Systemen, zu wachsen und sich zu entwickeln. Durch die Integration neuer Elemente und die Schaffung neuer Verbindungen kann das System größere und vielfältigere Aufgaben bewältigen.
Kritische Komplexität: Eine wichtige Grenze
Ein wichtiger Aspekt ist die Konzeptualisierung kritischer Komplexitätsgrenzen. Ein System kann nicht komplexer sein als seine kritische Komplexität, es sei denn, es werden zusätzliche Strukturen hinzugefügt. In der Nähe dieser kritischen Komplexitätsgrenzen werden Systeme besonders zerbrechlich und können plötzlich zusammenbrechen.
Quantitative Ansätze in der Komplexitätsforschung
Eine fundierte Metrik ermöglicht es, über bloße Spekulationen hinauszugehen und eine Grundlage für sinnvolle wissenschaftliche Untersuchungen und praktisches Komplexitätsmanagement zu schaffen.
Die Rolle der Metrik als Brücke zwischen Physik und Informationstheorie
Die Metrik fungiert als Brücke zwischen Physik und Informationstheorie, indem sie nicht nur die dynamische Interaktion zwischen Struktur und Entropie erfasst, sondern auch die Informationsmenge, die aus der Struktur resultiert.
Interaktion zwischen Struktur und Entropie
Obwohl Struktur und Entropie gegensätzliche Tendenzen repräsentieren, sind sie miteinander verflochten und beeinflussen sich gegenseitig auf komplexe Weise:
- Dynamisches Gleichgewicht: In vielen Systemen gibt es ein dynamisches Gleichgewicht zwischen der Schaffung von Struktur und der Zunahme von Entropie. Lebende Organismen beispielsweise erhalten ihre Struktur (Ordnung) durch kontinuierliche Energiezufuhr, die jedoch auch Entropie erzeugt.
- Energie und Information: Struktur erfordert Energie und Information, um aufrechterhalten zu werden. Die Erhaltung oder Schaffung von Struktur reduziert lokal die Entropie, kann aber die globale Entropie erhöhen. Zum Beispiel verwendet ein Kühlschrank Energie, um innerhalb des Geräts eine niedrige Temperatur (niedrige Entropie) aufrechtzuerhalten, während die Umgebung durch die abgeführte Wärme eine höhere Entropie erfährt.
- Evolution und Innovation: In evolutionären Prozessen führt die Schaffung neuer Strukturen zu einer Zunahme der Komplexität. Diese neuen Strukturen müssen effizient mit Entropie umgehen, um stabil zu bleiben. Innovationen entstehen oft durch die Erhöhung der strukturellen Komplexität, die jedoch durch die daraus resultierende Entropie begrenzt wird.
- Kritische Komplexität: Ein System kann nur bis zu einem bestimmten Punkt strukturell komplexer werden, bevor die Entropie es destabilisiert. Dies wird als kritische Komplexität bezeichnet. Jenseits dieses Punktes wird das System fragil und anfällig für Zusammenbrüche.
Von der System-DNA zu mess- und steuerbaren Hub-Parametern
Schritt 1: Bestimmen der relevanten Parameter eines Systems – Beispiele
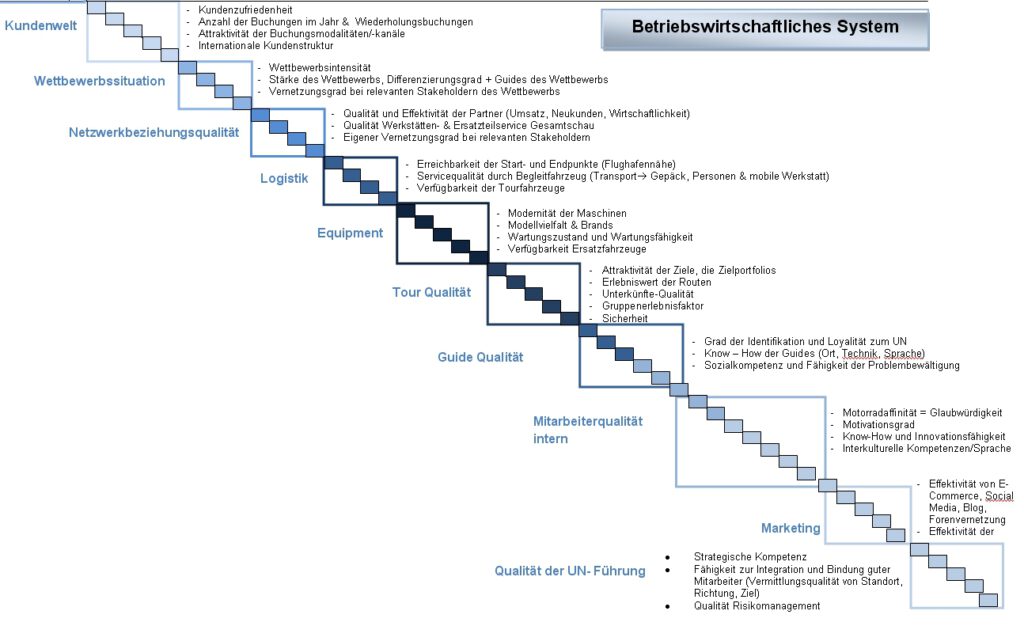
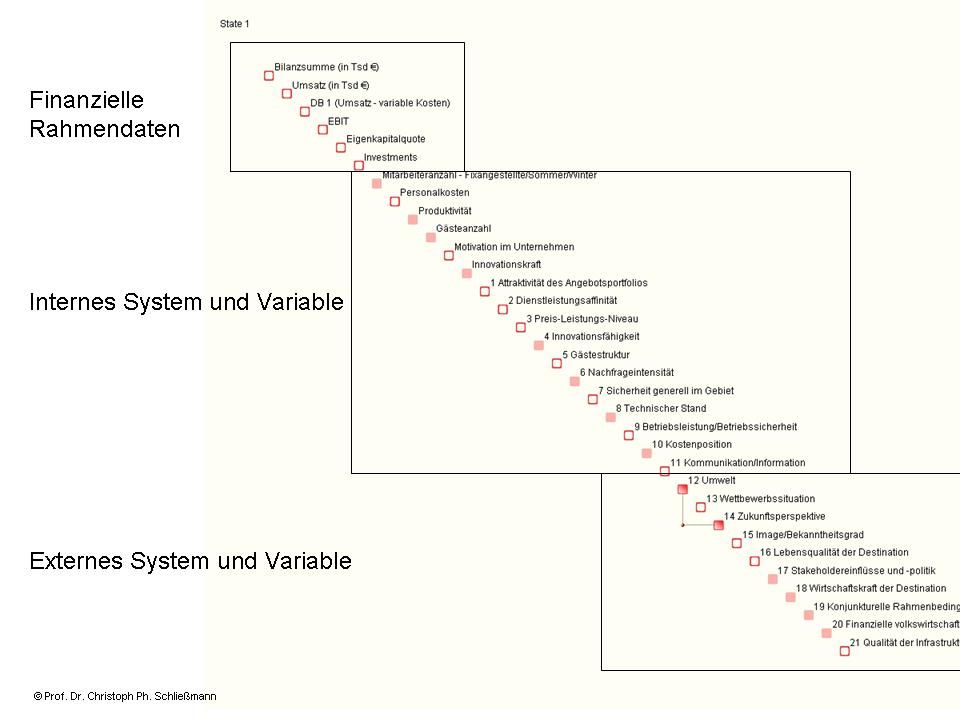
Schitt 2: Bestimmen von quantifizierbaren Messdaten für die relevanten Parameter
Schritt 3: Komplexitätsmetrik der strukturierten Information
Schritte 4: Identifizieren der Steuerungs-Hubs im System – Konzentration darauf
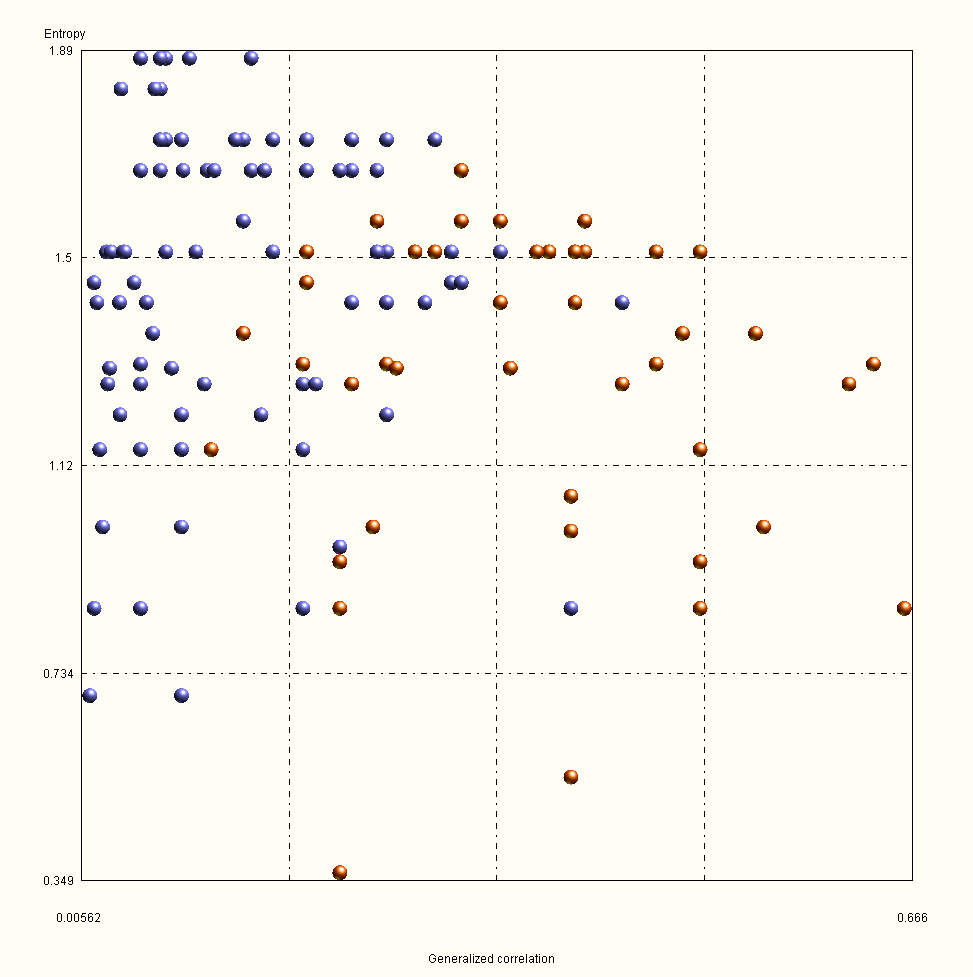
Mit „OntoSpace“, dem Werkzeug zur System- und Komplexitätsanalyse, das Christoph Schließmann zusammen mit seinem Technologiepartner Ontonix bei der Entwicklung der Interdependency-Methode integriert hat, ist es möglich, neben exakten Daten die Fuzzylogik anzuwenden. Erfahrungen aus der Vergangenheit werden ebenso wie Planperioden der nahen Zukunft in Kennzahlen überführt. Das Instrument arbeitet modellfrei, und die ermittelten Systemdaten werden ohne Modellfilterung so verarbeitet, wie sie vorliegen. Der Schlüssel zur modellfreien „Analyse“ ist, die Information zu „sehen“ und nicht zu „analysieren“.
Entropie misst den Grad der Desorganisation von Information. OntoSpace verarbeitet multidimensionale Information über ihre Datenentropie in eine übergeordnete „Bildstruktur“, wobei diese auf Pixel reduziert wird. Dabei ergeben sich Regionen mit hoher Datendichte (Cluster), Zonen mit sehr geringer Dichte, leere Regionen und einige isolierte Punkte (Ausreißer). Bilder mit Struktur übertragen mehr Informationen als chaotische Bilder. Obwohl einige Bilder geringe Entropie haben – sie sind sehr „organisiert“ –, übertragen sie dennoch nur wenige Informationen. Dies liegt daran, dass Entropie nicht nur den Grad an Chaos misst, sondern auch an Information. Ein einzelnes, schwarzes Pixel hat die niedrigst mögliche Entropie, aber um den Preis jeglicher fehlender Informationen. Über die Informationsstrukturen lassen sich Eigenschaften des Systems bestimmen: das Vorliegen von Komplexität als Produkt von Agilität und Robustheit. Es lassen sich Aussagen darüber treffen, welche Variablen in welchem Ausmaß zur Komplexität beitragen, welche Gesamt-Komplexität das System aufweist, wo seine Mindest- und seine kritische Grenzkomplexität liegen und wie es um seine Robustheit bestellt ist, Negativeinflüsse abzufedern. Die Identifikation von Komplexität erfolgt u.a. über eine Knock-out-Technik, ein Prozess der Quantifizierung, der über die Auswirkungen der einzelnen Variablen auf die gesamte Komplexität eines Systems Aufschluss gibt. Zunächst wird die Gesamtkomplexität des Systems berechnet, dann jede Variable aus dem System entfernt und die Komplexität immer wieder situativ neu berechnet. Der Unterschied zwischen den beiden Komplexitätswerten wird mit dem ursprünglichen Wert der Komplexität korreliert. Danach wird die Variable wieder in den System-Datensatz rückgeführt und die nächste Variable entfernt.
Das System-Rating misst den Komplexitätsgrad innerhalb eines Minimums und kritischen Maximums (hohe Fragilität des Systems), die Robustheit wie den Agilitätsgrad und zeigt die HUBS der größten Interdependenz wie hier am Beispiel eines Automotive-Unternehmens der Parameter 12 von 25.
Hier im Beispiel ist mit 210 die System-Entropie, also der Grad der Unordnung und Unsicherheit in den Systemrelationen relativ hoch. Je mehr verschiedene Korrelations- und Anordnungsmöglichkeiten die Parameter in einem System bieten, um si mehr steigt das Maß der Entropie.
Der Komplexitätsgrad liegt bei einem Minimum von 6 bei 13 von 16 Punkten und ist damit im beginnenden kritischen Bereich, was auch die Robustheit und den Resilienzgrad von knapp 72% relativiert. Ein solches System ist hochanfällig!
Es gilt daher die kritischen Vernetzungen und Parameter genau zu hinterfragen und über Szenarien für die Lebensfähigkeit des Systems in der Zukunft zu deuten.
Diese Ratingmatrix zeigt im Überblick die Interdependenzen der Parameter sowie ihren Beitrag zur Komplexität. Zu jeder einzelnen Beziehung gibt es umfangreiche Informationen.
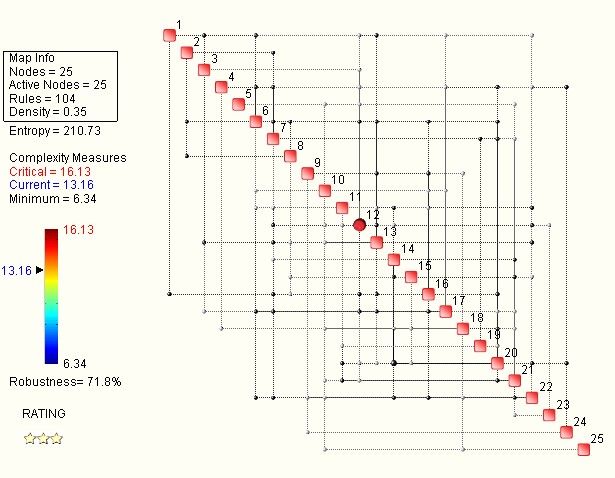
Jede einzelne Interdependenz kann nun hinsichtlich Beziehungsqualität und Entropie analysiert werden: